2ch,5chまとめ,数学,数学

1: みつを ★
2020/02/25(火) 02:43:55.65 ID:uM7/U9sB9
2020年2月24日
「三平方の定理」がひと目で分かる展示が面白いと話題に 「視覚的にわかる」「こういうのが学校にあったら」
液体の動きで見るとよりワクワクできます。
[宮原れい,ねとらぼ]
中学生の頃に習った「三平方の定理(ピタゴラスの定理)」がひと目で分かる展示が「面白い」「すごい」とTwitterで話題です。
三平方の定理は、直角三角形における3本の辺のうち、最も長い辺・斜辺を「c」、それ以外の2つの辺を「a」「b」としたとき、
「c」の2乗=「a」の2乗+「b」の2乗
――が成り立つというもの。この文章や式だと、どういうことかイマイチ分かりにくかったりしますが、投稿された展示ではビジュアルだけで「三平方の定理」が成り立っている様子を表現しています。青い液体を使った面積の足し算がわかりやすい!
(リンク先に続きあり)

8: 名無しさん@1周年
2020/02/25(火) 02:49:23.04 ID:Z4CuALXZ0
>>3
>>1
んー、やっぱ、わかりやすさ!
ここが大事ってことよね
38: 名無しさん@1周年
2020/02/25(火) 03:02:09.05 ID:lcpa0m3X0
>>1
これもう、アルキメデスとピタゴラス完全に分かんなくなる奴だわ
39: 名無しさん@1周年
2020/02/25(火) 03:05:36.59 ID:Sb5+jW7u0
>>1
偶然だろ?て言われたらこの実験だけじゃ説明つかんだろ
40: 名無しさん@1周年
2020/02/25(火) 03:06:02.17 ID:gIdDA+MS0
>>1
どういうこと? 逆に全然わからない
2: 名無しさん@1周年
2020/02/25(火) 02:46:05.93 ID:5hpIYfp90
なんでそこを中心に選んだのか、さっぱり分からない!
3: 名無しさん@1周年
2020/02/25(火) 02:46:07.99 ID:NPGRjQcb0
生理用品のCMのときの液体やん
4: 名無しさん@1周年
2020/02/25(火) 02:46:51.27 ID:cPq2yktU0
三平方の定理の証明は、ニュートンの証明とアインシュタインの証明がカッコよくて好き。
23: 名無しさん@1周年
2020/02/25(火) 02:57:28.63 ID:/Qtx3bP50
>>4
数学のこと語るだけで自分が頭良いと思えるんだろ?
そういうところが凡人なんだよw
5: 高篠念仏衆さん
2020/02/25(火) 02:47:33.24 ID:v/4/t15L0
三色旗の定理?🇷🇴
6: 名無しさん@1周年
2020/02/25(火) 02:48:27.36 ID:hgpBpKrE0
ピタゴラスが気づいたタイルの並びのほうが分かりやすいと思うが
7: 名無しさん@1周年
2020/02/25(火) 02:48:48.44 ID:gQX10Yzm0
これでなにか分かった気分にさせられるのって怖いね
9: 名無しさん@1周年
2020/02/25(火) 02:49:44.13 ID:CHRYW0EN0
方眼紙に書けばわかりやすいのに
10: 名無しさん@1周年
2020/02/25(火) 02:49:48.69 ID:fM/CeDyI0
公式を覚えるのには役に立つだろうけど、一番大切なそこに至るまでの過程が分からん
13: 名無しさん@1周年
2020/02/25(火) 02:50:39.21 ID:CHRYW0EN0
>>10
だから方眼紙に書けばめちゃわかりやすい
11: 名無しさん@1周年
2020/02/25(火) 02:50:11.79 ID:o9vNDn/70
ボール置いて数えたらいいじゃん
工作レベルで理解できないなら CGにしろw
12: 名無しさん@1周年
2020/02/25(火) 02:50:22.36 ID:cUHMeB8a0
まったく証明になっとらん やり直し
14: 名無しさん@1周年
2020/02/25(火) 02:51:10.94 ID:GrXBTBNd0
数学的理解にはむしろ遠くなってないかコレ
15: 名無しさん@1周年
2020/02/25(火) 02:51:18.22 ID:TjCIb/Hi0
視覚情報なんかなくたって
計算式で論理的に計算ができるようになるのが数学なんだよ
そんなもんに頼ってたら一生数学なんかできん
19: 名無しさん@1周年
2020/02/25(火) 02:54:43.28 ID:GrXBTBNd0
>>15
いや、むしろ視覚に置き換えるのは頻繁にやるだろ?
16: 名無しさん@1周年
2020/02/25(火) 02:52:00.16 ID:6N8WuZls0

見ただけじゃ2乗がどうのとかはわからんだろwww
20: 名無しさん@1周年
2020/02/25(火) 02:55:22.93 ID:E8+8Y1HF0
>>16
これはひっくり返すと上の視覚に
疑似おしっこが移動するやつなんじゃ?
35: 名無しさん@1周年
2020/02/25(火) 03:01:19.00 ID:arEWhhMH0
>>20
えうれか
17: 名無しさん@1周年
2020/02/25(火) 02:52:06.95 ID:tWtiABjY0
二乗が正方形の面積になってるのがいいね
この場合の奥行きは無視しても
そもそも二乗ってなんやねんて感じだもんな
21: 名無しさん@1周年
2020/02/25(火) 02:56:25.54 ID:xmRl35Iu0
視覚的に面白いとは思うが
一緒に紹介されてる図の方が「ほう!」ってなる人が多い気がする
32: 名無しさん@1周年
2020/02/25(火) 03:00:07.64 ID:S0ue4lge0
>>21
まったくだな
49: 名無しさん@1周年
2020/02/25(火) 03:12:19.30 ID:brxYhOLb0
>>21
これいいじゃん
対称性もあってわかりやすい
22: 名無しさん@1周年
2020/02/25(火) 02:57:13.00 ID:KB1u39Cq0
はいはいはい、これね、メロンの公式ね
24: 名無しさん@1周年
2020/02/25(火) 02:57:54.63 ID:hgpBpKrE0
でも白と青の面積が同じだと一目でわかるかこれ
25: 名無しさん@1周年
2020/02/25(火) 02:58:10.76 ID:4LgaukUo0
分かった気になるだけチャウチャウ?
26: 名無しさん@1周年
2020/02/25(火) 02:58:29.09 ID:+JSauGr40
CAD使えばいいよ
27: 名無しさん@1周年
2020/02/25(火) 02:58:40.17 ID:0Wm3w7aa0
何がひと目で分かるのかが分からない俺文系
28: 名無しさん@1周年
2020/02/25(火) 02:58:44.55 ID:4w/gxTvM0
多い日も安心
29: 名無しさん@1周年
2020/02/25(火) 02:59:05.50 ID:S0ue4lge0
これでは何も理解できない
30: 名無しさん@1周年
2020/02/25(火) 02:59:11.86 ID:bMyxpAy30
どこがいいのかわからん
昔のままの方法のほうがいいじゃん
31: 名無しさん@1周年
2020/02/25(火) 02:59:28.26 ID:8fm9Ggvk0
角錐とか円錐の体積で1/3を掛けるのはなぜ?
の説明と同じ
ごまかしです
33: 名無しさん@1周年
2020/02/25(火) 03:00:31.07 ID:9JYi28ay0
よくわからないんだが
34: 名無しさん@1周年
2020/02/25(火) 03:00:45.22 ID:6c6qVZjA0
色々難点があると思うな
正方形を見て2乗をとらえられるか
スキマの三角形が直角三角形だとわかるか
あと正方形が大小に分かれているので大小がつくものだと勘違いしやすい
36: 名無しさん@1周年
2020/02/25(火) 03:01:25.83 ID:2ChBoIJi0
何でこうなるかの説明になってない
37: 名無しさん@1周年
2020/02/25(火) 03:02:06.60 ID:jZvUhcdO0
タイルのほうが感覚でわかるやん
50: 名無しさん@1周年
2020/02/25(火) 03:12:27.59 ID:uDxL6ywW0
>>1
単に面白いってだけで、定理がひと目で分かるとは思えんね
>>37
それ
41: 名無しさん@1周年
2020/02/25(火) 03:08:17.22 ID:y1X0mEuE0
互いに素なピタゴラス数の整数解は無限にある
○か×か
48: 名無しさん@1周年
2020/02/25(火) 03:12:05.70 ID:6c6qVZjA0
>>41
○
これは文字式で考えないと証明できんよね
42: 名無しさん@1周年
2020/02/25(火) 03:08:38.02 ID:cUHMeB8a0
Twitter民の偏差値は5ちゃんねら以下って事で
43: 名無しさん@1周年
2020/02/25(火) 03:08:39.99 ID:kV+33IzT0
まーたぶん分からん人にこれ見せても分からん
44: 名無しさん@1周年
2020/02/25(火) 03:09:12.56 ID:xo0Y1FtC0
見てもわからなかった。
45: 名無しさん@1周年
2020/02/25(火) 03:09:30.05 ID:gyuvr+L00
あんまり感心せんね
これだけだとたまたま上手くいく大きさを選んだだけと言われる
いつでも成り立つということの証明にはならない
46: 名無しさん@1周年
2020/02/25(火) 03:11:16.49 ID:OXi1bJlu0
トリックじゃないのか。とか言ってみた。
厚み(深さ)を変えれば、どうにでもなるし。
47: 名無しさん@1周年
2020/02/25(火) 03:11:51.77 ID:CwuRl8bO0
この模型を見ても、なぜ直角三角形の斜辺の二乗が直角を挟んだ二辺の二乗の和に等しくなるのか俺はわからん
ウィキペディアのこれの方がまだわかるようなわからねえような

引用元: ・【数学】「三平方の定理」がひと目で分かる展示が面白いと話題に 「視覚的にわかる」「こういうのが学校にあったら」
数学者や教師になりたい人以外には公式の成り立ちなんて覚えても何も意味無い
この定理を使って仕事をする人たちは公式自体を記憶していれば十分
設計屋が言うんだから間違いない


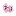 http://nlab.itmedia.co.jp/nl/articles/2002/24/news030.html
http://nlab.itmedia.co.jp/nl/articles/2002/24/news030.html
 http://twitter.com/asunokibou/status/1230844325040250880?s=2...
http://twitter.com/asunokibou/status/1230844325040250880?s=2...





ディスカッション
コメント一覧
まだ、コメントがありません